Well, it was bound to happen eventually - I got COVID-19. It hasn’t been a fun ride, but likely would have been worse without my two Pfizer vaccinations and Moderna booster. Symptoms started the day before Thanksgiving (11/24). Initially it was a really bad cough, chills, and a fever of 102F. Generally I’m very fortunate in my health, and this is easily the most sick I’ve been in several years. Unfortunately two self-administered rapid antigen tests and another at urgent care reported negatives (presumably false-negatives), so I was given Tamiflu and sent on my way. On a hunch related to some very bland tasting tikka masala, I took another test on the 27th which came back positive. Since then I’ve been testing myself daily, and today I finally tested negative.
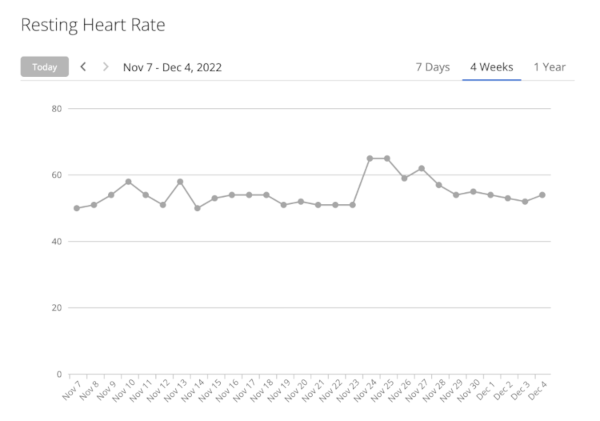
In addition to the expected symptoms, the jump in my resting heartrate was pronounced. As the graph below shows, on the first day (11/24) my resting heartrate jumped from it’s normal value of 51 bpm to 65 bpm, and it’s been slowly coming back to normal ever since. I don’t know if this is because of the impact of COVID-19 on the heart, or simply because my sleep was poor (and deep sleep is normally where the lowest HR occurs). I suspect the former, as lately I’ve been sleeping well but my heartrate hasn’t quite returned to normal.
Because of this experience I was curious about the false-positive and false-negative rates for rapid antigen tests. I’ve had a bit of trouble finding this data so I thought I’d compile what I learned…
Study #1, False Positives
False-Positive Results in Rapid Antigen Tests for SARS-CoV-2
Summarized findings:
- Tests: 903,408
- Negative: 902,086
- Positive: 1322
- True positive: 860
- False positive: 462
- False positive rate (assume true negatives = 902086): 462/(462+902086) = 0.05%
Study #2, False Negatives
Summarized findings:
- Tests: 723
- Negative: 677
- Positive: 46
- True negative: 650
- False negative: 27
- False negative rate (assume true positives = 46): 27/(27+46) = 37%
Analysis
To makes sense of this, we need to be Bayesians.
First, what are the chances that if I test positive I’m actually well?
P(well|positive_test) = P(positive_test|well)*P(well)/P(positive_test)
Sticking in some numbers from study #1:
| Probabiity | Fraction | Decimal |
|---|---|---|
| P(positive_test|well) | 462/(462+902086) | 0.00051 |
| P(well) | (902086+462)/903408 | 0.999 |
| P(positive_test) | 1322/903408 | 0.0015 |
| P(well|positive_test) | 462/(462+902086)*(902086+462)/903408/(1322/903408) | 35% |
Second, what are the chances that if I test negative that I’m actually sick?
P(sick|negative_test) = P(negative_test|sick)*P(sick)/P(negative_test)
Sticking in some numbers from study #2:
| Probabiity | Fraction | Decimal |
|---|---|---|
| P(negative_test|sick) | 27/(46+27) | 0.37 |
| P(sick) | (46+27)/723 | 0.10 |
| P(negative_test) | 677/723 | 0.94 |
| P(sick|negative_test) | 27/(46+27)*(46+27)/723/(677/723) | 4.0% |
Well, I was sick and tested negative, so either:
- I was one of the 4.0%
- I had a mild virus initially and COVID found its way in to my weakened immune system.
- The background rate of COVID was higher than in the study. For example if P(sick) were 0.3 and P(negative_test) were 0.7, then the statistic would become 15% (I find this unlikely)
In closing…
As of today my symptoms are largely gone, only a small lingering cough which mostly comes out when I’m running or walking. Before COVID I had been increasing my running mileage, and it’s a bit of a setback to my training to have taken so long off, and still not be 100%. Regardless, I’m happy to be done with it, and grateful for all the medical technologies which made my life easier.