One major pitfall I see electrical engineers and computer scientists fall into when building digital filters is a lack of understanding of signal aliasing. A simple phenomenon that most everyone learns in their DSP 101 class in undergrad.
For example, say you’re given a simple task, design a digital low pass filter to attenuate a signal above 10 Hz. We might decide to design a first order filter with a 1 Hz bandwidth, which should give fantastic attenuation at 10 Hz. Let’s give it a try.
First, the continuous time filter in the Laplace domain
\[\frac{Y}{U} = \frac{2\pi}{s + 2\pi}\]We will discretize the filter to run at 100 Hz, that should be plenty fast for our 1 Hz filter. Using a bilinear transform we arrive at:
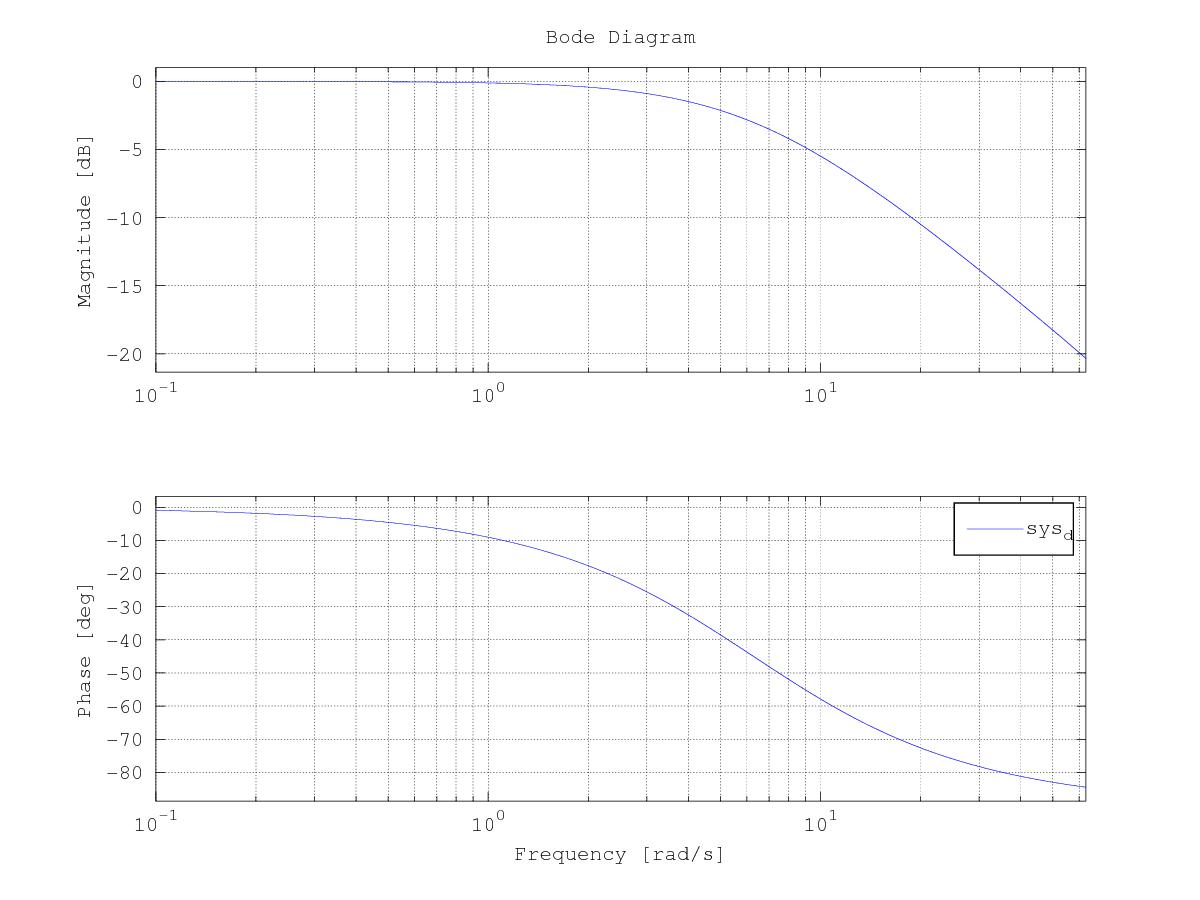
\[y[n] = 0.03046 u[n] + 0.03046 u[n-1] + 0.9391 y[n-1]\]The bode plot of our digital filter suggests fantastic attenuation at 10 Hz (about -20 dB).
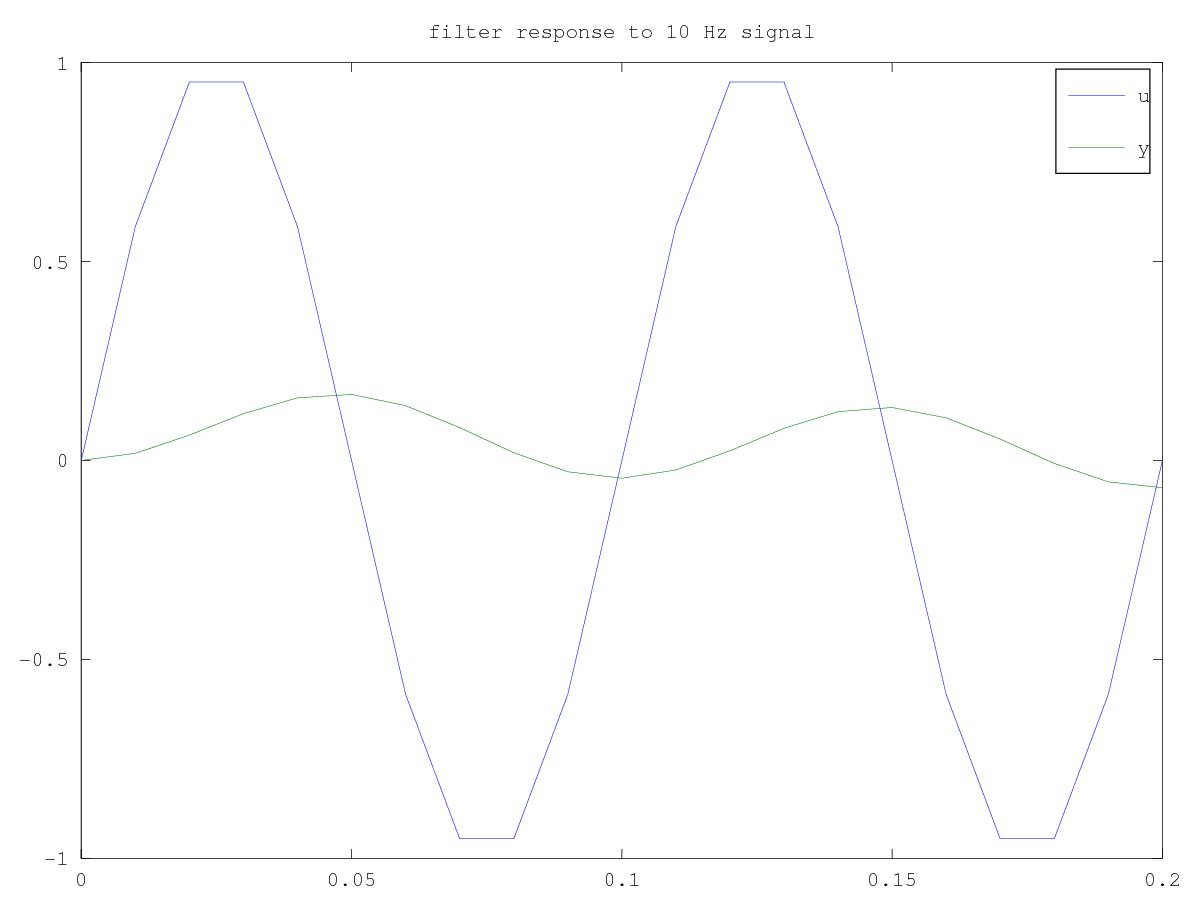
And the response to a 10 Hz signal looks very attenuated indeed.
But the phenomenon of aliasing presents a problem here. Specifically, a high frequency signal filtered below its Nyquist frequency can look like a low frequency signal to our filter, which in turn will not be able to reject it. The Nyquist sampling theorem states that to reconstruct a signal with frequency \(f\) we need to sample at no less than \(2f\). For our example that means we can only reconstruct signals accurately which are less than \(\frac{100 Hz}{2} = 50 Hz\).
Alias frequencies have the following relationship to the base frequency \(f\), sampling rate \(f_s\), and any integer \(N\).
\[f_{alias} = | f - N f_s |\]What if our filter experiences a signal with a frequency of 99.9 Hz? We think our filter will reject the signal, as 99.9 Hz is much larger than the bandwidth of our filter (1 Hz).
But what about the alias frequencies? From the math above we expect the 99.9 Hz signal to alias down to \(99.9 - 100 = 0.1\) Hz which is beneath our filter bandwidth and won’t be rejected. The plot below shows the filter response.
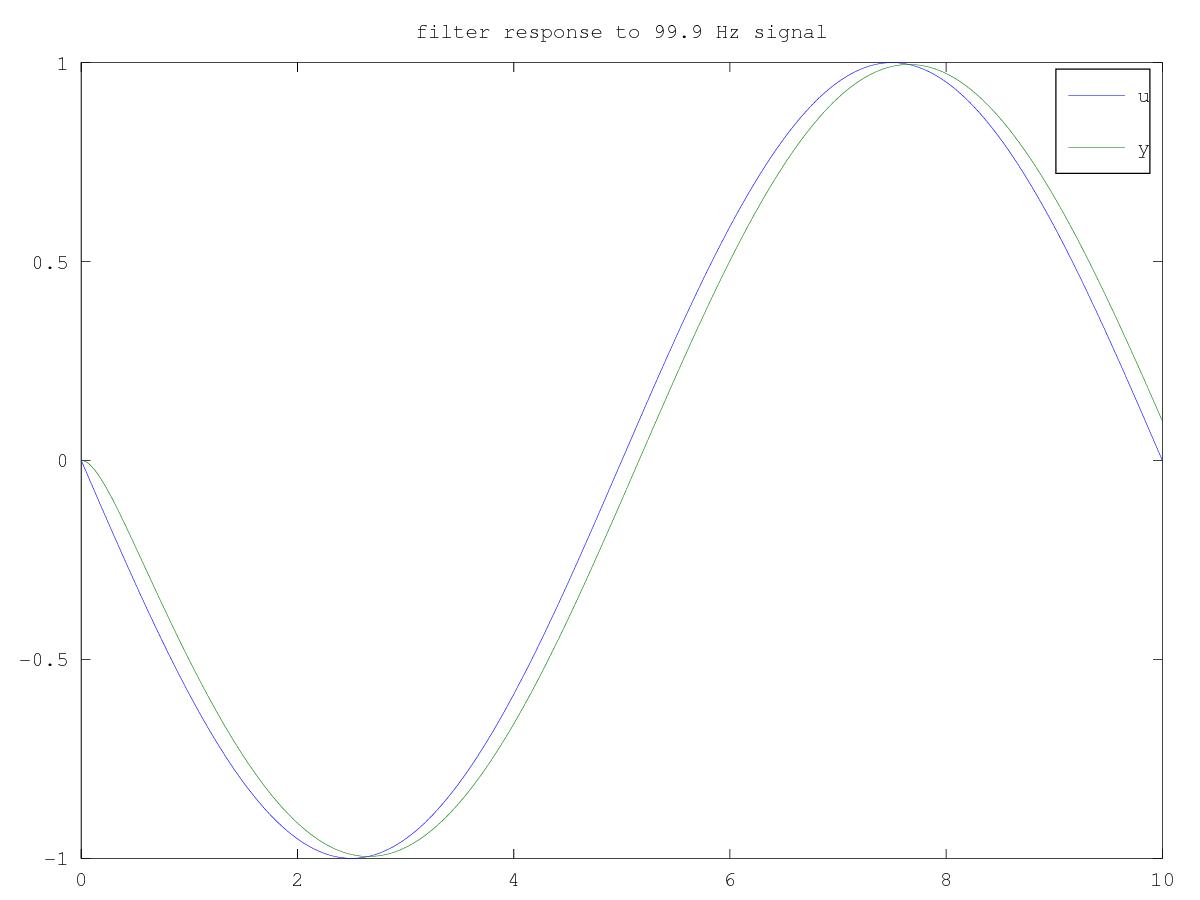
That is clearly no good. The input signal, truly at 99.9 Hz, has aliased down to 0.1 Hz which our 1 Hz filter is happy to pass through nearly unchanged. How do we mitigate against this?
- Use an analog filter (mechanical or electrical) as a “first-pass” filter which has a bandwidth that is less than the Nyquist rate of your digital filter. This ensures that no signals which might be aliased down to a lower frequency will make it to the digital filter.
- If you can establish a true upper bound to the sorts of frequencies you will experience, \(f_{ub}\), then try to sample your digital filter faster than \(2f_{ub}\).